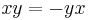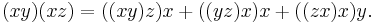Malcev algebra
For the Lie algebras or groups, see Malcev Lie algebra.
In mathematics, a Malcev algebra (or Maltsev algebra or Moufang–Lie algebra) over a field is a nonassociative algebra that is antisymmetric, so that
and satisfies the Malcev identity
They were first defined by Anatoly Maltsev (1955).
Examples
- Any Lie algebra is a Malcev algebra.
- Any alternative algebra may be made into a Malcev algebra by defining the Malcev product to be xy − yx.
- The imaginary octonions form a 7-dimensional Malcev algebra by defining the Malcev product to be xy − yx.
References
- Alberto Elduque and Hyo C. Myung Mutations of alternative algebras, Kluwer Academic Publishers, Boston, 1994, ISBN 0-7923-2735-7
- V.T. Filippov (2001), "Mal'tsev algebra", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=M/m062170
- Mal'cev, A. I. (1955), "Analytic loops" (in Russian), Mat. Sb. N.S. 36 (78): 569–576, MR0069190